Answer:
The friction factor is 0.303.
Step-by-step explanation:
The flow velocity (
 ), measured in meters per second, is determined by the following expression:
), measured in meters per second, is determined by the following expression:
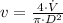 (1)
(1)
Where:
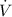 - Flow rate, measured in cubic meters per second.
- Flow rate, measured in cubic meters per second.
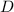 - Diameter, measured in meters.
- Diameter, measured in meters.
If we know that
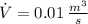 and
and
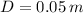 , then the flow velocity is:
, then the flow velocity is:

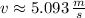
The density and dinamic viscosity of the glycerin at 20 ºC are
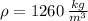 and
and
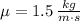 , then the Reynolds number (
, then the Reynolds number (
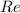 ), dimensionless, which is used to define the flow regime of the fluid, is used:
), dimensionless, which is used to define the flow regime of the fluid, is used:
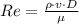 (2)
(2)
If we know that
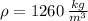 ,
,
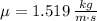 ,
,
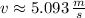 and
and
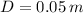 , then the Reynolds number is:
, then the Reynolds number is:
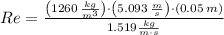

A pipeline is in turbulent flow when
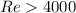 , otherwise it is in laminar flow. Given that flow has a laminar regime, the friction factor (
, otherwise it is in laminar flow. Given that flow has a laminar regime, the friction factor (
 ), dimensionless, is determined by the following expression:
), dimensionless, is determined by the following expression:
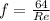
If we get that
 , then the friction factor is:
, then the friction factor is:
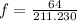

The friction factor is 0.303.