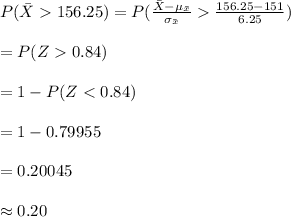Question

In the library on a university campus, there is a sign in the elevator that indicates a limit of 16 persons. Furthermore, there is a weight limit of 2500 lb. Assume that the average weight of students, faculty, and staff on campus is 151 lb, that the standard deviation is 25 lb, and that the distribution of weights of individuals on campus is approximately normal. If a random sample of 16 persons from the campus is to be taken:

a. What is the expected value of the sample mean of their weights?
b. What is the standard deviation of the sampling distribution of the sample mean weight?
c. What average weights for a sample of 16 people will result in the total weight exceeding the weight limit of 2500 lb?
d. What is the chance that a random sample of 16 persons on the elevator will exceed the weight limit?

Answer 1

Explained below.

Explanation:

According to the Central Limit Theorem if an unknown population is selected with mean μ and standard deviation σ and appropriately huge random samples (n > 30) are selected from this population with replacement, then the distribution of the sample means will be approximately normally.

Then, the mean of the sample means is given by,

`\mu_(\bar x)=\mu`

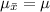
And the standard deviation of the sample means is given by,

`\sigma_(\bar x)=(\sigma)/(√(n))`

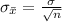
a

The expected value of the sample mean of their weights is same as the population mean, μ = 1515 lbs.

b

The standard deviation of the sampling distribution of the sample mean weight is:

`\sigma_(\bar x)=(\sigma)/(√(n))=(25)/(√(16))=6.25`

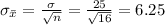
c.

The average weights for a sample of 16 people will result in the total weight exceeding the weight limit of 2500 lbs. is:

`\text{Average Weight}=(2500)/(16)=156.25`

d

Compute the probability that a random sample of 16 persons on the elevator will exceed the weight limit as follows:

`P(\bar X > 156.25)=P((\bar X-\mu_(\bar x))/(\sigma_(\bar x))>(156.25-151)/(6.25))\\\\=P(Z>0.84)\\\\=1-P(Z<0.84)\\\\=1-0.79955\\\\=0.20045\\\\\approx 0.20`