Answer:
![\huge\boxed{f^(-1)(x) = \sqrt[3]{(x-8)/(4)}}](https://img.qammunity.org/2021/formulas/mathematics/high-school/o9yaiajxghqvffrpkfbetxdyrwtc2rjd80.png)
Explanation:
In order to find the inverse of a function, we need to follow a series of steps.
1. Write the function in the form
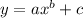
2. Swap where the x and y values are
3. Solve for y
4. Convert into
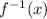 form
form
So first, we can write
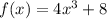 as
as
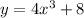 .
.
Now we need to swap where the x and y variables are. This makes our equation
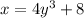 .
.
To find the inverse, we now need to solve for y in this equation.
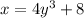
- Subtract 8 from both sides:
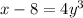
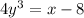
- Divide both sides by 4:
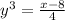
- Take the cube root of each side:
![y = \sqrt[3]{(x-8)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/3up12l8l911cu1x20cla5obj4ffrykco9l.png)
- Convert into
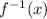 form
form
Therefore, the inverse of this function is
![f^(-1)(x) = \sqrt[3]{(x-8)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/2tqx1vuohri3euijmtmiiau6ekg6bssob9.png) .
.
Hope this helped!