Answer:
The equation of the line tangent to the graph of f at x = -1 is
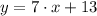 .
.
Explanation:
From Analytical Geometry we know that the tangent line is a first order polynomial, whose form is defined by:
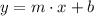 (1)
(1)
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 - Slope, dimensionless.
- Slope, dimensionless.
 - Intercept, dimensionless.
- Intercept, dimensionless.
The slope of the tangent line at
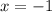 is:
is:
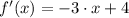 (2)
(2)
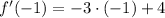

If we know that
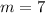 ,
,
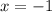 and
and
 , then the intercept of the equation of the line is:
, then the intercept of the equation of the line is:


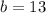
The equation of the line tangent to the graph of f at x = -1 is
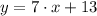 .
.