Question

The mid segment of the triangle is 5x-1. Find the value of x.

Answer 1

The value of x = 6

Explanation:

The Midsegment of a triangle theorem states that the midsegment of a triangle is parallel to the third side of the triangle and it’s always equal to the one half or 1/2 of the length of the third side.

Now we can conclude that from the given triangle, the length of midsegment is 5x-1 which is parallel to the side of length 58, and will always equal to 1/2 of the length of the side of length 58.

Mathematically it means:

`5x-1\:=\:(58)/(2)`

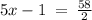
solving to find the length of x

`5x-1=29`

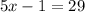
Add 1 to both sides

`5x-1+1=29+1`

`5x=30`

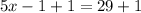
Divide both sides by 5

`(5x)/(5)=(30)/(5)`

`x=6`

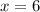
Therefore, the value of x = 6