Answer:
a. E(X) = 0.333 minutes
b.
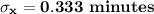
c. 0.9986
Explanation:
a.
To find the mean time between counts
Let X be the random variable that illustrates the time between the successive log-ons, then X is exponential with the rate
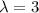 log-ons per minute.
log-ons per minute.
i.e.
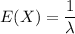
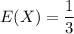
E(X) = 0.333 minutes
b. Since X is attributed to an exponential distribution, The standard deviation between counts is:
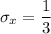
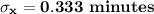
c.
Given that;
The average number of count per minute = 3
The value of X such that P(X < x) = 0.95 can be calculated as;
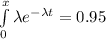
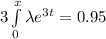
![\bigg [ -e^(3t)\bigg ]^x_0 = 0.95](https://img.qammunity.org/2021/formulas/mathematics/college/a58is5r2lahtowv3l1bqy1s7sx5fw58u3u.png)

-3x = ㏑ (0.05)
-3x = - 2.9957
x = -2.9957/ -3
x = 0.9986
The value of x = 0.9986