It looks like the function is defined by
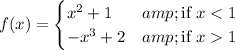
which we immediately is discontinuous at x = 1 because f(1) is not defined. One of the strict inequalities should probably have ≥ or ≤ involved.
In order for f(x) to be continuous at x = 1, we need have the one-sided limits agree:


They do not agree, so f(x) is indeed discontinuous at x = 1, regardless of what value we pick for f(1). Graphically this corresponds to a jump discontinuity, where f(x) jumps from 2 down to 1 as x varies past x = 1.
[A and D]