Question

3. Given A(3,5), B(7, 10), C(0, 2), and D(1, a),

determine the value of a for which:
a) Line AB is parallel to line CD.
b) Line AB is perpendicular to line CD.
please help!! i’m failing grade 10 precal and i need this❤️ will give 15 points

Answer 1

1) if Line AB is parallel to line CD then value of a is: a=3

2) if Line AB is perpendicular to line CD then value of a is: a=1

Explanation:

We are given A(3,5), B(7, 10), C(0, 2), and D(1, a) we need to find value of a for which:

We can use slope formula:
`Slope=(y_2-y_1)/(x_2-x_1)` to find value of a according to conditions given.

We are given:

`x_1=3, y_1=5, x_2=7, y_2=10 \ for \ line \ AB \ and \\\x_1=0, y_1=2, x_2=1, y_2=a \ for \ line \ CD \`

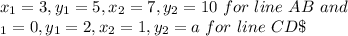
a) Line AB is parallel to line CD.

When 2 lines are parallel there slope is same so, using this we can find value of a

`Slope \ of \ line \ AB = Slope \ of \ line \ CD`

`(y_2-y_1)/(x_2-x_1)= (y_2-y_1)/(x_2-x_1)\\(10-5)/(7-3)=(a-2)/(1-0) \\(5)/(5)=(a-2)/(1)\\1=a-2\\a=1+2\\a=3`

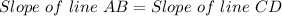
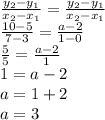
So, if Line AB is parallel to line CD then value of a is: a=3

b) Line AB is perpendicular to line CD.

When 2 lines are perpendicular there slopes are opposite of each other so, using this we can find value of a

`Slope \ of \ line \ AB =-(1)/(Slope \ of \ line \ CD)`

`(y_2-y_1)/(x_2-x_1)=-(1)/( (y_2-y_1)/(x_2-x_1)) \\(y_2-y_1)/(x_2-x_1)=-(x_2-x_1)/(y_2-y_1)\\(10-5)/(7-3)=-(1-0)/(a-2) \\(5)/(5)=-(1)/(a-2)\\1=-(1)/(a-2)\\a-2=-1\\a=-1+2\\a=1`

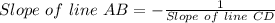
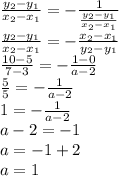
So, if Line AB is perpendicular to line CD then value of a is: a=1