Answer:
The viscosity

Step-by-step explanation:
From the given information:
Time t = 1.55 s
The radius of capillary = 5.00 μm /2
The pressure drop ΔP = 2.45 kPa
The length of the capillary = 2.00 mm
∴
The viscosity of the blood flow can be calculated by using the formula:
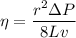
where;
v = L/t
Then;
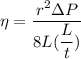

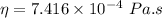
To (N.s/m²)
