Question

An electrochemical cell is composed of pure nickel and pure iron electrodes immersed in solutions of their divalent ions at room temperature (25°C). If the concentrations of Ni2+ and Fe2+ ions are 0.002 M and 0.40 M, respectively, what voltage is generated at 25°C? (The respective standard reduction potentials for Ni and Fe are −0.250 V and −0.440 V.)

Answer 1

0.758 V.

Step-by-step explanation:

Hello!

In this case, case when we include the effect of concentration on an electrochemical cell, we need to consider the Nerst equation at 25 °C:

`E=E\°-(0.0591)/(n) log(Q)`

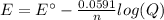
Whereas n stands for the number of moles of transferred electrons and Q the reaction quotient relating the concentration of the oxidized species over the concentration of the reduced species. In such a way, we can write the undergoing half-reactions in the cell, considering the iron's one is reversed because it has the most positive standard potential so it tends to reduction:

`Fe^(2+)+2e^-\rightarrow Fe^0\ \ \ E\°=0.440V\\\\Ni^0\rightarrow Ni^(2+)+2e^-\ \ \ E\°=-0.250V`

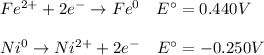
It means that the concentration of the oxidized species is 0.002 M (that of nickel), that of the reduced species is 0.40 M and there are two moles of transferred electrons; therefore, the generated potential turns out:

`E=(0.440V+0.250V)-(0.0591)/(2) log((0.002M)/(0.40M) )\\\\E=0.758V`

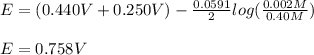
Beat regards!