Question

Solve the the equation tan(x+pi/3) = sqrt 3/3 over the interval [0, 2].

Answer 1

Rewrite the right side as √3/3 = 1/√3, and recall that tan(x) = 1/√3 when x = π/6. Then since tan is π-periodic, taking the inverse tan of both sides gives

`\tan\left(x + \frac\pi3\right) = \frac1{\sqrt3} \implies \tan^(-1)\left(\tan\left(x + \frac\pi3\right)\right) = \tan^(-1)\left(\frac1{\sqrt3}\right) + n\pi`

`\implies x + \frac\pi3 = \frac\pi6 + n\pi`

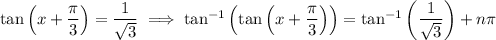
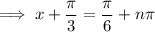
where n is any integer. Solving for x, we get

`x = -\frac\pi6 + n\pi`

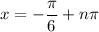
and the solutions in the interval [0, 2π] are x = 5π/6 and x = 11π/6 (for n = 1 and n = 2).