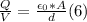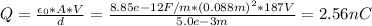Answer:
2.56 nC
Step-by-step explanation:
- By definition, the capacitance is expressed by the following relationship between the charge stored on one of the plates of the capacitor and the potential difference between them, as follows:
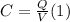
- For a parallel-plate capacitor, assuming a uniform surface charge density σ, if the area of the plates is A, the charge on one of the plates can be written as follows:

- Assuming an uniform electric field E, the potential difference V can be expressed as follows:
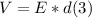
where d is the distance between plates.
- Applying Gauss 'Law to a closed surface half within one plate, half outside it, we find that E can be written as follows:
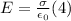
- Replacing (4) in (3), and (2) in (1), we can express the capacitance C as follows:
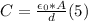
- Taking (1) and (5), as both left sides are equal each other, the right sides are also equal, so we can write the following equality: