Question

A mass of 100 g is tied to the end of an 80.0-cm string and swings in a vertical circle about a fixed center under the influence of gravity. The speed of the mass at the top of the swing is 3.50 m/s. What is the speed of the mass at the bottom of its swing?

Answer 1

the speed of the mass at the bottom of its swing is 6.61m/s

Step-by-step explanation:

Applying energy conservation

`(1)/(2)m(Vlowest)^2 = mg(2R) + (1)/(2)m(Vtop)^2`

There is no potential energy at the bottom as the body will have a kinetic energy there.

h= 2R = 1.6m as the diameter of the circle will represent the height in the circle.

g = 9.8m/s^2

m will cancel out, so the net equation becomes.

`((Vbottom)^2)/(2) = 2gR + ((Vtop)^2)/(2)`

=
`2*9.8*0.8 + ((3.5)^2)/(2)`

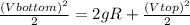
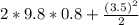
= 15.68+ 6.125

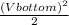`((Vbottom)^2 )/(2)` = 21.805

(Vb)^2 = 2*21.805

= 43.64

Vb = 6.61m/s