Question

Conservationists have despaired over destruction of tropical rain forest by logging, clearing, and burning." These words begin a report on a statistical study of the effects of logging in Borneo. Here are data on the number of tree species in 12 unlogged forest plots and 9 similar plots logged 8 years earlier:

Col1 Unlogged 2218 222015121 13 13 1913 19 15

Col2 Logged 17 4 181418151510 12 Use the data to give a 90% confidence interval for the difference in mean number of species between unlogged and logged plots. Compute degrees of freedom using the conservative methoo. Interval: ________to__________.

Answer 1

Answer: -8.16 to 15.84

Explanation: Confidence Interval is an interval in which we are a percentage sure the true mean is in the interval.

A confidence interval for a difference between two means and since sample 1 and sample 2 are under 30, will be

`x_(1)-x_(2)` ±
`t.S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2)) }`

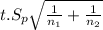
where

x₁ and x₂ are sample means

t is t-score

`S_(p)` is estimate of standard deviation

n₁ and n₂ are the sample numbers

The estimate of standard deviation is calculated as

`S_(p)=\sqrt{((n_(1)-1)s_(1)^(2)+(n_(2)-1)s_(2)^(2))/(n_(1)+n_(2)-2) }`

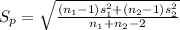
where

s₁ and s₂ are sample standard deviation of each sample

Degrees of freedom is:

`df=n_(1)+n_(2)-2`

df = 12 + 9 - 2

df = 19

Checking t-table, with 90% Confidence Interval and df = 19, t = 1.729.

The mean and standard deviation for 12 unlogged forest plots are 17.5 and 3.53, respectively.

The mean and standard deviation for 9 logged plots are 13.66 and 4.5, respectively.

Calculating estimate of standard deviaton:

`S_(p)=\sqrt{((12-1)(3.53)^(2)+(9-1)(4.5)^(2))/(12+9-2) }`

`S_(p)=\sqrt{(299.07)/(19) }`

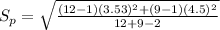
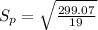
`S_(p)=` 15.74

The difference between means is

`x_(1)-x_(2)` = 17.5 - 13.66 = 3.84

Calculating the interval:

`t.S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2)) }` =
`1.729.15.74.\sqrt{(1)/(12) +(1)/(9) }`

`t.S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2)) }` =
`27.21\sqrt{(21)/(108) }`

`t.S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2)) }` =
`27.21√(0.194)`

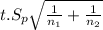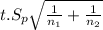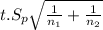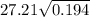
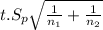`t.S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2)) }` = 12

Then, interval for the difference in mean is 3.84 ± 12, which means the interval is between:

lower limit: 3.84 - 12 = -8.16

upper limit: 3.84 + 12 = 15.84

The interval is from -8.16 to 15.84.