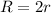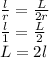Answer:
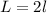 where
where
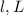 denote arc lengths of two circles
denote arc lengths of two circles
Explanation:
Let
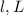 denote arc lengths of two circles,
denote arc lengths of two circles,
 denote corresponding radii and
denote corresponding radii and
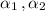 denote the corresponding central angles.
denote the corresponding central angles.
So,
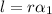 and
and
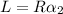
This implies
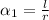 and
and
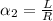
As each circle has an arc where the measures of the corresponding central angles are the same,
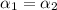
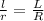
As radius of one circle is twice the radius of the other circle,