Question

Which of the following could be the perimeters of the three squares below?

A 12ft, 16 ft and 20 ft
B 20 ft, 16 ft and 24 ft
C) 40 ft, 80 ft and 120 ft
D 16 ft, 24 ft and 28 ft

Answer 1

Option (A)

Explanation:

Option (A).

Since, perimeter of a square = 4×(side)

Perimeters of 3 squares = 12 ft, 16 ft and 20 ft

Side lengths of three squares will be =
`(12)/(4), (16)/(4),(20)/(4)`

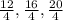
= 3 ft, 4 ft and 5 ft

If these sides are the measures of the sides of the given right triangle,

(Hypotenuse)² = (leg 1)² + (leg 2)²

5² = 4² + 3²

25 = 16 + 9

25 = 25

True.

Therefore, these are the sides of the given right triangle.

Option (B).

Perimeters of three squares are 20 ft, 16 ft and 24 ft.

Sides lengths of three squares =
`(20)/(4),(16)/(4), (24)/(4)`

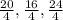
= 5 ft, 4 ft and 6 ft

By Pythagoras theorem,

6² = 4² + 5²

36 = 61

False.

Therefore, these sides are not of the given right triangle.

Option (C)

Perimeters of the squares = 40 ft, 80 ft and 120 ft

Side lengths of the squares = 10 ft, 20 ft and 30 ft

If these sides are the sides of the given right triangle, they will follow the Pythagoras theorem.

By Pythagoras theorem,

(30)² = (10)² + (20)²

900 = 500

False.

Option (D)

Perimeters of the given squares are 16 ft, 24 ft and 28 ft.

Side lengths of these squares will be 4 ft, 6 ft and 7 ft.

If these sides form a right triangle they will follow the Pythagoras theorem.

By Pythagoras theorem,

7² = 4² + 6²

49 = 16 + 36

49 = 52

False.

Therefore, these are not the sides of a right triangle.

Option (A) will be the answer.