Question

For the functions given below, find and simplify completely: g(x+h)-g(x)/h (here, h is some parameter)

a. g(x) = 2x +6
b. g(x) = 2x^2-x

Answer 1

a. 2

b. 4x -1 +2h

Explanation:

We can find the difference quotient for the given cases by first solving for the difference quotient in the general case. That solution can then be applied to the given cases.

__

general solution

For f(x) = ax² +bx +c, the difference quotient is ...

`(f(x+h)-f(x))/(h)=((a(x+h)^2+b(x+h)+c)-(ax^2+bx+c))/(h)\\\\=((ax^2+2axh+ah^2+bx+bh+c)-(ax^2+bx+c))/(h)=(2axh+ah^2+bh)/(h)\\\\=\underline{2ax+b+ah}`

__

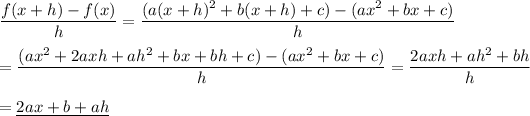
a.

For g(x) = 2x+6, we have a=0, b=2, c=6. Substituting these values into the above formula, we find ...

(g(x+h) -g(x))/h = 2·0·x² +2 +0·h

(g(x+h) -g(x))/h = 2

__

b.

For g(x) = 2x² -x, we have a=2, b=-1, c=0. Substituting these values into the above formula, we find ...

(g(x+h) -g(x))/h = 2·2·x +(-1) +2·h

(g(x+h) -g(x))/h = 4x -1 +2h