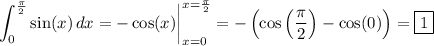Question

Help me solve the control problem urgently​

Answer 1

1. My Russian is a bit rusty. I think you're asking to find the antiderivatives in the first part:

а)
`\displaystyle \int 2x^n - 5x \, dx = \boxed{\frac2{n+1} x^(n+1) - \frac52 x^2 + C}`

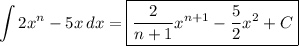
This follows from the power rule for differentiation,

`\frac d{dx} x^n = n x^(n-1)`

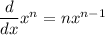
I'm not sure what the power on the first term is, so I just use a general real number n. This solution is correct as long as n ≠ -1; otherwise we would have

`\displaystyle \int 2x^(-1) - 5x = 2\ln|x| - \frac52 x^2 + C`

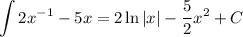
б) Using the fact that

`\frac d{dx} \sin(x) = \cos(x)`

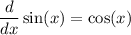
as well as the power rule from part (a),

`\displaystyle \int 3 \cos(x) - x \, dx = \boxed{3 \sin(x) - \frac12 x^2 + C}`

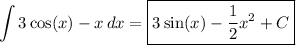
в) By the chain rule,

`\frac d{dx} \sin(5x) = 5 \cos(5x)`

`\frac d{dx} \cos(3x) = -3 \sin(3x)`

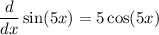
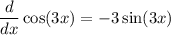
Hence

`\displaystyle \int \cos(5x) - \frac16 \sin(3x) \, dx = \boxed{\frac15 \sin(5x) + \frac1{18} \cos(3x) + C}`

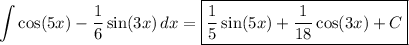
2. These just look like standard definite integrals. Using the known derivatives mentioned in part (1) in conjunction with the fundamental theorem of calculus, we have

a)

`\displaystyle \int_0^1 x^2 \, dx = \frac13 x^3 \bigg|_(x=0)^(x=1) = \frac13 (1^3 - 0^3) = \boxed{\frac13}`

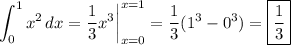
б)

`\displaystyle \int_0^(\frac\pi2) \sin(x) \, dx = -\cos(x) \bigg|_(x=0)^(x=\frac\pi2) = -\left(\cos\left(\frac\pi2\right) - \cos(0)\right) = \boxed{1}`