Answer:
The probability that the mean test score is greater than 290
P(X⁻ > 290 ) = 0.0217
Explanation:
Step(i):-
Mean of the Population (μ) = 281
Standard deviation of the Population = 34.4
Let 'X' be a random variable in Normal distribution
Given X = 290
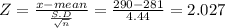
Step(ii):-
The probability that the mean test score is greater than 290
P(X⁻ > 290 ) = P( Z > 2.027)
= 0.5 - A ( 2.027)
= 0.5 - 0.4783
= 0.0217
The probability that the mean test score is greater than 290
P(X⁻ > 290 ) = 0.0217