Question

10 workers produce 30 complex elements in 10 days. In how many days would 5

workers produce 24 elements?

Answer 1

Given:

10 workers produce 30 complex elements in 10 days.

To find:

The number of days, in which 5 workers produce 24 elements.

Solution:

According to the question, let as assume

`n_1=10`

`w_1=30`

`d_1=10`

`n_2=x`

`w_2=24`

`d_2=5`

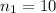
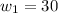
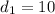
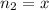
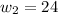
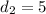
where, n is number of workers, w is work done, and d is number of days.

We have, a formula,

`(n_1* d_1)/(w_1)=(n_2* d_2)/(w_1)`

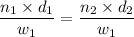
Substituting the values in the above formula, we get

`(10* 10)/(30)=(x* 5)/(24)`

`(10)/(3)=(5x)/(24)`

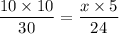
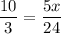
Isolate variable x.

`(10)/(3)* (24)/(5)=(5x)/(24)* (24)/(5)`

`(240)/(15)=x`

`16=x`

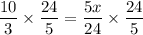
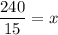
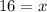
Therefore, the required number of days is 16.