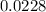Question

The amount of gasoline G sold each month to customers at Bob's Exxon station in downtown Navasota is a random variable. This random variable G can be described as having a normal distribution with mean 2500 gallons and a standard deviation of 250 gallons (and there is no seasonal variation in sales). Exxon will give Bob an all-expense paid trip to College Station, including a free dinner at Burger King, if his station pumps more than 3000 gallons in any one month.

Required:

What is the probability that Bob will win that wonderful trip on the basis of his gasoline sales this month?

Answer 1

The probability is
`0.0228`

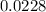
Explanation:

Let's start by defining the random variable
`G` as :

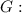`G:` '' The amount of gasoline sold each month to customers at Bob's Exxon station in downtown Navasota ''

Therefore, if
`X` is a continuous random variable that has a normal distribution, we write
`X` ~
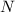`N` ( μ , σ )

Where ''μ'' is the mean and ''σ'' is the standard deviation.

For the random variable
`G` we write :

`G` ~
`N(2500,250)`

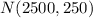
We need to find
`P(G>3000)`

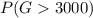
In order to calculate this, we are going to standardize the variable. This means, finding the equivalent probability in a normal random variable

`Z` ~
`N(0,1)`

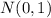
We perform this because the random variable
`Z` ~
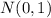`N(0,1)` is tabulated in any book or either you can find the table on Internet.

To standardize the variable we need to subtract the mean and then divide by the standard deviation ⇒

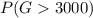`P(G>3000)` ⇒ P[ (G - μ) / σ >
`(3000-2500)/(250)` ] ⇒
`P(Z>2)`

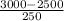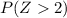
Because (G - μ) / σ ~
`Z`

Finally,
`P(G>3000)=P(Z>2)` ⇒
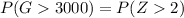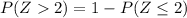`P(Z>2)=1-P(Z\leq 2)` = 1 - Φ(2)

Where '' Ф(x) =
`P(X\leq x)` '' represents the cumulative function of
`Z`

Looking for Φ(2) in any table,

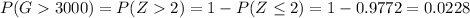`P(G>3000)=P(Z>2)=1-P(Z\leq 2)=1-0.9772=0.0228` ≅ %2.28

We found out that the probability is
`0.0228`