The given linear system is:
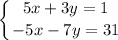
Linear systems can be solved using either elimination or substitution. However, the question is asking to solve using elimination, so I will use that method.
When eliminating, you can either eliminate x or y. In this system, x is much easier to eliminate. The x variable in the first equation is 5x, and in the second equation, it is -5x. Since 5 and -5 cancel each other out, you don't need to do anything other than add.
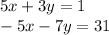
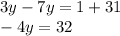
Lastly, you need to leave the variable y alone. The variable is currently -4y or -4 times y. To remove it, you need to do the opposite of it, which is dividing by -4.
Divide both sides by -4:
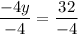
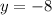
Now that you have the value of y, substitute it into one of the equations to find x. I will be substituting it into the first equation.

Open the parentheses and multiply:
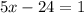
Move 24 to the other side to leave the variable alone:
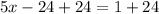
You will be adding since you're "removing" it by doing the opposite of it.
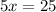
Lastly, divide both sides by 5 to leave x alone.
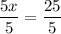

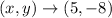
The answer is (5, -8).