Given:
Principal value = $65,550
Rate of interest = 3% compounded every six month
To find:
The taken to have $100,000 in Jack's account.
Solution:
The formula for amount is
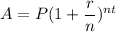
where, P is principal, r is rate of interest, n is number of times interest compounded in an year, t is time in number of years.
Interest compounded every six month. It means, interest compounded 2 times in an year.
Substitute A=100000, r=0.03 and n=2 in the above formula.
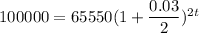

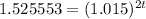
Taking log on both sides.
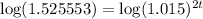
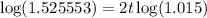
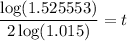
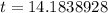
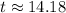
Therefore, after 14.18 year the amount will reach at $100,000 or we can say that in 15th year the amount will reach at $100,000.