Question

A ball filled with an unknown material starts from rest at the top of a 2 m high incline that makes a 28o with respect to the horizontal. The ball rolls without slipping down the incline and at the bottom has a speed of 4.9 m/s. How many revolutions does the ball rotate through as it rolls down the incline

Answer 1

Searching in google I found the total mass and the radius of the ball (m = 1.5 kg and r = 10 cm) which are needed to solve the problem!

The ball rotates 6.78 revolutions.

Step-by-step explanation:

Searching in google I found the total mass and the radius of the ball (m = 1.5 kg and r = 10 cm) which are needed to solve the problem!

At the bottom the ball has the following angular speed:

`\omega_(f) = (v_(f))/(r) = (4.9 m/s)/(0.10 m) = 49 rad/s`

Now, we need to find the distance traveled by the ball (L) by using θ=28° and h(height) = 2 m:

`sin(\theta) = (h)/(L) \rightarrow L = (h)/(sin(\theta)) = (2 m)/(sin(28)) = 4.26 m`

To find the revolutions we need the time, which can be found using the following equation:

`v_(f) = v_(0) + at`

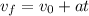
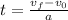`t = (v_(f) - v_(0))/(a)` (1)

So first, we need to find the acceleration:

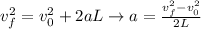`v_(f)^(2) = v_(0)^(2) + 2aL \rightarrow a = (v_(f)^(2) - v_(0)^(2))/(2L)` (2)

By entering equation (2) into (1) we have:

`t = (v_(f) - v_(0))/((v_(f)^(2) - v_(0)^(2))/(2L))`

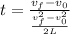
Since it starts from rest (v₀ = 0):

`t = (2L)/(v_(f)) = (2*4.26 m)/(4.9 m/s) = 1.74 s`

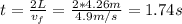
Finally, we can find the revolutions:

`\theta_(f) = (1)/(2) \omega_(f)*t = (1)/(2)*49 rad/s*1.74 s = 42.63 rad*(1 rev)/(2\pi rad) = 6.78 rev`

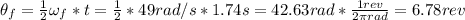
Therefore, the ball rotates 6.78 revolutions.

I hope it helps you!