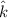Answer:
0.546
Step-by-step explanation:
From the given information:
The force on a given current-carrying conductor is:
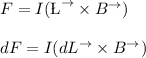
where the length usually in negative (x) direction can be computed as
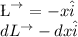
Now, taking the integral of the force between x = 1.0 m and x = 3.0 m to get the value of the force, we have:

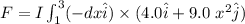
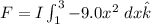
![F = I (9.0) \bigg [(x^3)/(3) \bigg ] ^3_1 \hat k](https://img.qammunity.org/2021/formulas/physics/college/xim2gqjfaom7cqpsoo730awkbownizh8k2.png)
![F = I (9.0) \bigg [(3^3)/(3) - (1^3)/(3) \bigg ] \hat k](https://img.qammunity.org/2021/formulas/physics/college/mqu7yp8v9mt4nbesr6uihd50avm0wkcu9t.png)
where;
current I = 7.0 A
![F = (7.0 \ A) (9.0) \bigg [(27)/(3) - (1)/(3) \bigg ] \hat k](https://img.qammunity.org/2021/formulas/physics/college/1if4415oxbnhfougqdy738yspy0nz47bb1.png)
![F = (7.0 \ A) (9.0) \bigg [(26)/(3) \bigg ] \hat k](https://img.qammunity.org/2021/formulas/physics/college/zpp1nj0lm6tt8iqgf0dg9t19o14ra55ahi.png)
F = 546 × 10⁻³ T/mT
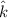
F = 0.546