Question

The linear parent function is transformed to create the new function g(x)=12f(x−13). What is the correct description of the transformations.

The new function g(x) is less steep than f(x) and shifted to the left 13 units.

The new function g of x is less steep than f of x and shifted to the left 13 units.


The new function g(x) is steeper than f(x) and shifted to the left 13 units.

The new function g of x is steeper than f of x and shifted to the left 13 units.


The new function g(x) is steeper than f(x) and shifted to the right 13 units.

The new function g of x is steeper than f of x and shifted to the right 13 units.


The new function g(x) is less steep than f(x) and shifted to the right 13 units

Answer 1

The new function g(x) is steeper than f(x) and shifted to the left 13 units.

Step-by-step explanation:

Given

`g(x) = 12f(x - 13)`

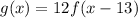
Required

Determine the relationship between f(x) and g(x)

First, we need to determine the direction which f(x) is shifted to (right or left)

For a function f(x)

f(x - h) implies that f(x) is shifted right by h units

So, f(x - 13) implies that f(x) is shifted right by 13 units

Next, we determine the steepness of f(x) and g(x)

We can assume that the steepness of f(x) is 1

The steepness of g(x) can be determined as follows:

`g(x) = 12f(x - 13)`

`g(x) = 12 * f(x - 13)`

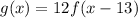
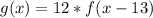
Hence, the steepness of g(x) is 12

Going by the analysis above:

g(x) is steeper and f(x) is shifted 13 units right to get g(x)