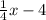Answer:
Explanation:
1). Let the equation of a line is,
y = mx + b
Here, m = slope of the line
b = y-intercept
From the graph attached,
Slope =
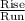 =
=

y-intercept = -2
Equation → y =
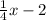
2). Slope of the line =
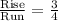
y-intercept 'b' = -3
Equation → y =
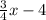
3). Slope of the line =

=
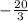
y-intercept = 5
Equation → y =
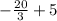
4). Slope of the line =
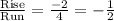
y-intercept = 4
Equation → y =
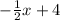
5). Since, line is passing through origin (0, 0)
y-intercept = 0
Slope =
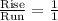
Equation → y = x
6). Slope of the line =
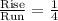
y-intercept = -4
Equation → y =