Final Answer:
- Equation 1: One solution
- Equation 2: Infinite solutions
- Equation 3: No solution
Step-by-step explanation:
Equation 1,
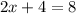 , is a linear equation with one variable and one solution. It can be solved by isolating the variable, yielding a unique solution. Equation 2,
, is a linear equation with one variable and one solution. It can be solved by isolating the variable, yielding a unique solution. Equation 2,
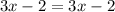 , is an identity where both sides are equal regardless of the value of x. This indicates infinite solutions since any value for x satisfies the equation.
, is an identity where both sides are equal regardless of the value of x. This indicates infinite solutions since any value for x satisfies the equation.
Equation 3,
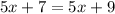 , leads to a contradiction when simplified, implying no solution. This happens when the variable disappears, and the statement becomes false. In detail, subtracting 5x from both sides leaves 7 = 9, which is not a true statement. Therefore, the system has no solution.
, leads to a contradiction when simplified, implying no solution. This happens when the variable disappears, and the statement becomes false. In detail, subtracting 5x from both sides leaves 7 = 9, which is not a true statement. Therefore, the system has no solution.
In summary, Equation 1 has one solution due to its linear nature, Equation 2 has infinite solutions as an identity, and Equation 3 has no solution because it leads to a contradiction during the simplification process. The different outcomes highlight the diverse possibilities in systems of linear equations.