Answer:
a) A´= A
b) θ₁´ = 29º, θ₂´ = - 169º , θ₃´ = -49º
Step-by-step explanation:
In this exercise you are asked to give the magnitudes and angles of the vectors from another system of
reference
a) The magnitudes
The magnitude of a vector, the size of which is a scalar, this does not depend on the reference system, since it is obtained by subtracting the coordinates of the end point minus the coordinate of the origin of the vector
A =
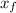 - x₀
- x₀
if the vectors are measured in another reference frame
x_{f}´ = xx_{f}- U
x₀´ = x₀ -U
where U is the distance between the two reference frames
A´ = x_{f}´ - x₀´
we substitute
A´ = (x_{f} - U) - (x₀-U) = x_{f} - x₀
A´ = A
it does not change
b) Angles
The given angles are measured from the positive part of the x axis in a counterclockwise direction, it is asked to give these angles from the x axis
θ₁ = 29º
does not change
θ₁´ = 29º
θ₂ = 191º
we measure clockwise
θ₂´ = θ₂ - 360
θ₂´ = 191 - 360
θ₂´ = - 169º
θ₃ =311º
we measure clockwise
θ₃´ = 311 -360
θ₃´ = -49º