Question

Force and Motion 4 of 40

II Pause
Susan and Michael travel on separate trains. Susan's train moves westward at a constant speed of 5 meters per second. Michael's train
moves eastward at a constant speed of 7 meters per second. How fast is Susan's train moving relative to Michael's train?

Answer 1

`V =2m/s`

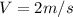
Step-by-step explanation:

Given:

Represent

- Susan's velocity with
`V_s`

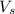
- Michael's velocity with
`V_m`

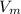
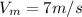`V_m = 7m/s` eastwards

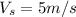`V_s = 5m/s` westwards

Required

Determine how fast is
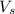`V_s` relative to
`V_m`

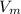
From the question, one train moves eastwards while the other moves westwards.

This means that travel in opposite travel and the relative speed (V) is calculated as:

`V = V_m - V_s`

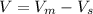
Substitute values for
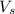`V_s` and
`V_m`

`V =7m/s - 5m/s`

`V =2m/s`

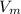
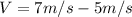
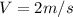
Hence, the Susan's train is moving 2m/s in relative to Michael's train