Question

A buffer solution is made that is 0.347 M in H2C2O4 and 0.347 M KHC2O4.

1. If Ka for H2C2O4 is 5.90E^-2, what is the pH of the buffer solution?
b. Write the net ionic equation for the reaction that occurs when 0.070 mol KOH is added to 1.00 L of the buffer solution.

Answer 1

1. pH = 1.23.

2.
`H_2C_2O_4(aq) +OH^-(aq)\rightarrow HC_2O_4^-(aq)+H_2O(l)`

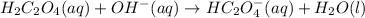
Step-by-step explanation:

Hello!

1. In this case, for the ionization of H2C2O4, we can write:

`H_2C_2O_4\rightleftharpoons HC_2O_4^-+H^+`

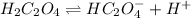
It means, that if it is forming a buffer solution with its conjugate base in the form of KHC2O4, we can compute the pH based on the Henderson-Hasselbach equation:

`pH=pKa+log(([base])/([acid]) )`

Whereas the pKa is:

`pKa=-log(Ka)=-log(5.90x10^(-2))=1.23`

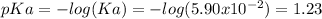
The concentration of the base is 0.347 M and the concentration of the acid is 0.347 M as well, as seen on the statement; thus, the pH is:

`pH=1.23+log((0.347M)/(0.347M) )\\\\pH=1.23+0\\\\pH=1.23`

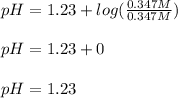
2. Now, since the addition of KOH directly consumes 0.070 moles of acid, we can compute the remaining moles as follows:

`n_(acid)=0.347mol/L*1.00L=0.347mol\\\\n_(acid)^(remaining)=0.347mol-0.070mol=0.277mol`

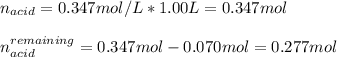
It means that the acid remains in excess yet more base is yielded due to the effect of the OH ions provided by the KOH; therefore, the undergone chemical reaction is:

`H_2C_2O_4(aq) +OH^-(aq)\rightarrow HC_2O_4^-(aq)+H_2O(l)`

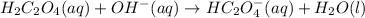
Which is also shown in net ionic notation.

Best regards!