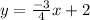Question

Which equation represents the same line as the points in the table

Answer 1

y = -3/4x + 2

Explanation:

we will choose any two points: (-4,5) and (0,2)

an linear equation should be like this y=ax+b

a is the slope, b is the y intercept

to find the slope we will use this formula: y1 - y2/x2 - x1

2-5/0-(-4) = -3/4

y = -3/4x + b

now you can find the answers by putting the values of x and y from the table

Answer 2

`y=(-3)/(4) x+2`

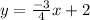
Explanation:

First, we can find the slope using the slope equation and two of the points.

Slope equation:

`m=(y2-y1)/(x2-x1)`

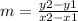
I'm going to use the first two points just so I can avoid the fraction... Substitute the x and y values into the equation.

`m=(2-5)/(0--4)`

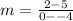
Simplify:

`m=(-3)/(4)`

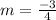
Now that we have the slope, all we need is the y-intercept. Luckily, it gives it to us in the table. The x value of y-intercepts will always be 0. Looking at the table, we see that the point where x=0 is (0,2). Thus, the y-intercept is 2. Your final equation is

`y=(-3)/(4) x+2`