Answer:
CV of Bank A = 6.4
CV of Bank B = 7.1
CV of Bank B is more than CV of Bank A
Explanation:
Bank A
6.6, 6.7, 6.7, 6.8, 7.0, 7.3, 7.5, 7.7, 7.8, 7.8

Standard deviation =
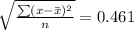
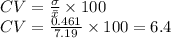
Bank B
4.0, 5.5, 5.8, 6.2, 6.6, 7.6, 7.7, 8.5, 9.4, 9.7

Standard deviation =
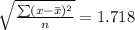
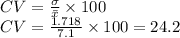
CV of Bank A = 6.4
CV of Bank B = 7.1
CV of Bank B is more than CV of Bank A