Question

In a designated VIP seating section there must be an odd number of seats in each row and each row must have two more seats than the one before it. The last requirement is that the front row must have one quarter the total seats in the back 2 rows combined. How many seats will be in each row?

Answer 1

Let n be the total number of rows and there are x seats is the 1st row where x is an odd natural number.

As each row must have 2 more seats than the one before it, so

Number of seats in 2nd row = x+2

Number of seats in 3rd row = x+2+2=x+2x2

Number of seats in 4th row = x+2+2+=x+2x3

Similarly, the number of seats in (n-1)th row =x+2x(n-1)

the number of seats in n^{th} row, i.e last row =x+2x n.

As the front row must have one-quarter of the total seats in the back 2 rows combined, so

`x =\frac 1 4 ( x+2*(n-1) + x+2* n) \\\\\Rightarrow 4x=2x+4n-6 \\\\\Rightarrow 4x-2x=4n-6 \\\\\Rightarrow 2x=4n-6 \\\\\Rightarrow x=2n-3\cdots(i)`

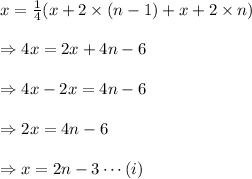
So, the number of seats in the 1st row, x, and the total number of seats, n, must satisfy the equation (i).

For
`x>0, n\geq 3.`

So, for n=3 rows

The number of seats in the 1st row, x= 2x3-3=3.

The number of seats in the 2nd row, = 3+2=5 as in subsequent rows, there will be 2 more seats.

and the number of seats in the 3rd row (last row)=5+2=7.

n can have any integral values satisfying
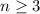`n\geq 3`.