Question

Write the equation of a possible rational

function that has an asymptote at x = 2, has a
point of discontinuity at x = -2.5, and passes
through (6, -3)

Plz show ALL steps

Answer 1

The graph has a removable discontinuity at x=-2.5 and asymptoe at x=2, and passes through (6,-3)

Explanation:

A rational equation is a equation where

`(p(x))/(q(x))`

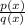
where both are polynomials and q(x) can't equal zero.

1. Discovering asymptotes. We need a asymptote at x=2 so we need a binomial factor of

`(x - 2)`

in our denomiator.

So right now we have

`(p(x))/((x - 2))`

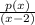
2. Removable discontinues. This occurs when we have have the same binomial factor in both the numerator and denomiator.

We can model -2.5 as

`(2x + 5)`

So we have as of right now.

`((2x + 5))/((x - 2)(2x + 5))`

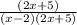
Now let see if this passes throught point (6,-3).

`((2x + 5))/((x - 2)(2x + 5)) = y`

`((17))/(68) = (1)/(4)`

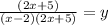
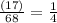
So this doesn't pass through -3 so we need another term in the numerator that will make 6,-3 apart of this graph.

If we have a variable r, in the numerator that will make this applicable, we would get

`((2x + 5)r)/((2x + 5)(x - 2)) = - 3`

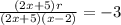
Plug in 6 for the x values.

`(17r)/(4(17)) = - 3`

`(r)/(4) = - 3`

`r = - 12`

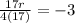
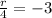
So our rational equation will be

`( - 12(2x + 5))/((2x + 5)(x - 2))`

or

`\frac{ - 24x - 60}{2 {x}^(2) + x - 10}`

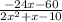
We can prove this by graphing