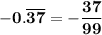Question

Enter your answer as a simplified fraction formatted like this: 42/53

the answer on there is wrong

Answer 1

`\displaystyle -0.\overline{37}=-(37)/(99)`

Explanation:

Convert a Repeating Decimal to a Fraction

We need to convert the following decimal to a fraction:

`-0.\overline{37}`

Let's call x to the given number:

`x=-0.\overline{37}`

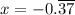
The number has two repeating (periodic) decimals, thus we multiply by 100:

`100x=-37.\overline{37}`

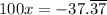
Note the decimals continue to repeat exactly like the original number.

Subtracting both expressións, the repeating decimals are simplified:

`100x - x = -37`

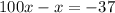
Operating:

99x=-37

Dividing by 99:

`\displaystyle x=-(37)/(99)`

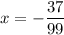
The fraction cannot be simplified, thus:

`\mathbf{\displaystyle -0.\overline{37}=-(37)/(99)}`