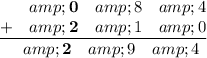Question

Explain how to multiply the following whole numbers 21 x 14

Answer 1

`\begin{matrix}\space\space&\textbf{2}&\textbf{1}\\ * \:&1&\textbf{4}\end{matrix}`

________

`\frac{\begin{matrix}\space\space&\textbf{0}&8&4\\ +&\textbf{2}&1&0\end{matrix}}{\begin{matrix}\space\space&\textbf{2}&9&4\end{matrix}}`

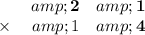
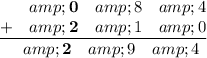
Explanation:

Given

`21\:* \:14`

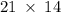
Line up the numbers

`\begin{matrix}\space\space&2&1\\ * \:&1&4\end{matrix}`

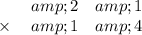
Multiply the top number by the bottom number one digit at a time starting with the ones digit left(from right to left right)

Multiply the top number by the bolded digit of the bottom number

`\begin{matrix}\space\space&\textbf{2}&\textbf{1}\\ * \:&1&\textbf{4}\end{matrix}`

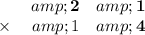
Multiply the bold numbers: 1×4=4

`\frac{\begin{matrix}\space\space&2&\textbf{1}\\ * \:&1&\textbf{4}\end{matrix}}{\begin{matrix}\space\space&\space\space&4\end{matrix}}`

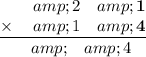
Multiply the bold numbers: 2×4=8

`\frac{\begin{matrix}\space\space&\textbf{2}&1\\ * \:&1&\textbf{4}\end{matrix}}{\begin{matrix}\space\space&8&4\end{matrix}}`

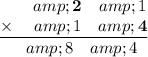
Multiply the top number by the bolded digit of the bottom number

`\frac{\begin{matrix}\space\space&\textbf{2}&\textbf{1}\\ * \:&\textbf{1}&4\end{matrix}}{\begin{matrix}\space\space&8&4\end{matrix}}`

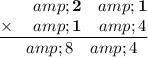
Multiply the bold numbers: 1×1=1

`\frac{\begin{matrix}\space\space&\space\space&2&\textbf{1}\\ \space\space&* \:&\textbf{1}&4\end{matrix}}{\begin{matrix}\space\space&\space\space&8&4\\ \space\space&\space\space&1&\space\space\end{matrix}}`

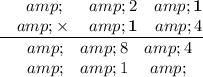
Multiply the bold numbers: 2×1=2

`\frac{\begin{matrix}\space\space&\space\space&\textbf{2}&1\\ \space\space&* \:&\textbf{1}&4\end{matrix}}{\begin{matrix}\space\space&\space\space&8&4\\ \space\space&2&1&\space\space\end{matrix}}`

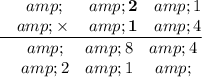
Add the rows to get the answer. For simplicity, fill in trailing zeros.

`\frac{\begin{matrix}\space\space&\space\space&2&1\\ \space\space&* \:&1&4\end{matrix}}{\begin{matrix}\space\space&0&8&4\\ \space\space&2&1&0\end{matrix}}`

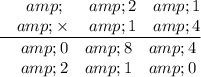
adding portion

`\begin{matrix}\space\space&0&8&4\\ +&2&1&0\end{matrix}`

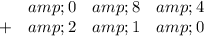
Add the digits of the right-most column: 4+0=4

`\frac{\begin{matrix}\space\space&0&8&\textbf{4}\\ +&2&1&\textbf{0}\end{matrix}}{\begin{matrix}\space\space&\space\space&\space\space&\textbf{4}\end{matrix}}`

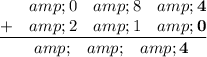
Add the digits of the right-most column: 8+1=9

`\frac{\begin{matrix}\space\space&0&\textbf{8}&4\\ +&2&\textbf{1}&0\end{matrix}}{\begin{matrix}\space\space&\space\space&\textbf{9}&4\end{matrix}}`

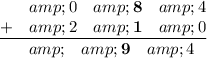
Add the digits of the right-most column: 0+2=2

`\frac{\begin{matrix}\space\space&\textbf{0}&8&4\\ +&\textbf{2}&1&0\end{matrix}}{\begin{matrix}\space\space&\textbf{2}&9&4\end{matrix}}`

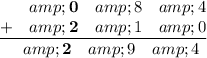
Therefore,

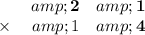
`\begin{matrix}\space\space&\textbf{2}&\textbf{1}\\ * \:&1&\textbf{4}\end{matrix}`

________

`\frac{\begin{matrix}\space\space&\textbf{0}&8&4\\ +&\textbf{2}&1&0\end{matrix}}{\begin{matrix}\space\space&\textbf{2}&9&4\end{matrix}}`