Answer:
The domain would include all the real values except
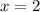 and the x for which
and the x for which
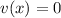 .
.
Hence, the restrictions would be:
and
Explanation:
Given
The domain of u(x) is the set of all real values except 0.
so
domain = (-∞, 0) U (0, ∞)
The domain of v(x) is the set of all real values except 2.
so
domain = (-∞, 2) U (2, ∞)
For the function composed function (u circle v) (x), we need to apply first the function
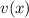 whose argument is (x), and then the function
whose argument is (x), and then the function
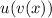 whose argument is
whose argument is
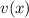 .
.
Please note that the domain of the composed function (u circle v) (x) must have to take into account the values for which both functions u(x) and v(x) are defined.
Therefore, the domain would include all the real values except
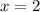 and the x for which
and the x for which
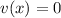 .
.
Hence, the restrictions would be:
and