Question

Write an equation in slope-intercept form for the line that passes through (6,- 3) and is parallel to y = -2x + 4 *

Answer 1

Answer: y = -2x + 9

Explanation:

We are asked to find an equation for a line that passes through (6,-3) and is parallel to y = -2x + 4.

Parallel lines have the same slope. So the new line also has a slope of -2.

Now we use the point slope formula

y - y1 = m(x - x1)

Substitute the values

y - (-3) = -2(x - 6)

y + 3 = -2x + 12

y = -2x + 12 - 3

y = -2x + 9

Therefore the new line’s equation is y = -2x + 9.

Answer 2

Write an equation in slope-intercept form for the line that passes through (6,- 3) and is parallel to y = -2x + 4.

__________________________________________________________

Parallel lines are lines with the same slope but different y-intercept.

Slope-intercept form is written as y=mx+b, where m is the slope and b is the y-intercept.

__________________________________________________________

The given line is y=-2x+4. A line parallel to this would have the same slope, which is -2. To find the y-intercept, plug the point into an equation in point-slope form.

`\displaystyle \text{Point-Slope Form} \rightarrow y-y_(1)=m(x-x_(1))`

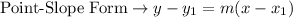
m is the slope, and since the slope is the same as the given line, m will be equal to 2.

The line is supposed to pass through a point, which is written as (x, y). In this line, it is supposed to pass (6, -3). x₁ will be the x value of the point, and y₁ will be the y value of the point. That means x₁ is 6 and y₁ is -3.

Substitute the values into the formula:

`y-y_(1)=m(x-x_(1)) \rightarrow y-(-3)=2(x-6)`

When subtracting a negative number from a number or variable, the sign will change, and the number will become positive.

`y-(-3)=y+3`

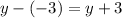
Here is the new equation:

`y-3=2(x-6)`

Distribute the 2 to everything in the parentheses. It will be 2 times x and 2 times -6. Remember that a positive number multiplied by a negative number is negative.

• Positive(+) times(×) positive(+) = positive(+)
• Positive(-) times(×) negative(-) = negative(-)
• Positive(+) divided(÷) by positive(+) = positive(+)
• Positive(+) divided(÷) by negative(-) = negative(-)

`2 * x=2x\\2 * -6=-12\\\\2(x-6)=2x-12`

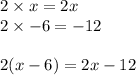
Rewrite the equation:

`y-3=2x-12`

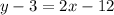
Lastly, you need to move -3 to the other side, as slope-intercept form is written as y=mx+b. You can move it by adding three(+3) to both sides, which is simply doing the opposite of it(-3+3=0).

`\displaystyle y-3+3=2x-12+3`

`y=2x-9`

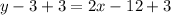
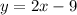
The answer to your question is
`\bf \displaystyle y=2x-9`.