Answer:
P = 1416 W
Step-by-step explanation:
- The tractor's motor needs to supply a power output that allow to pull the bale at a constant speed, so the pull up force must be equal to the net force pulling down on the bale.
- This force has two components, the component of the weight along the incline, and the friction force opposing to the relative movement between the bale and the incline, as follows:
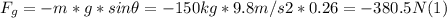
- The kinetic friction force, can be expressed as follows:

- The normal force, must be equal and opposite to the component of the weight perpendicular to the incline surface, as the normal force is always perpendicular to the surface, and it's upward.
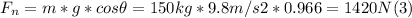
- Replacing (3) in (2), we have:
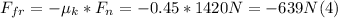
- Adding (4) and (1) we have the net force that must be equal and opposite to the supplied by the tractor's motor:
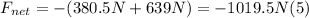
- We can express the power as the product of the force (assumed constant) times the speed, as follows:
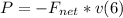
- Since we have the force in N, and the speed in km/h, we need first to convert km/h to m/s:
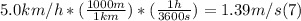
- Replacing (7) and (5), in (6), we get:
