Answer:
a) Stone v_{y} = - 7.25 ft / s , vₓ = 0.362 ft / s
b) tennis ball v_{y} = -3.16 ft / s , vₓ = 0.634 ft / s
c) golf ball v_{y} = - 1,536 ft / s, vx = 0.634 ft / s
2) golf ball
Step-by-step explanation:
1) The average speed is defined with the displacement interval in the given time interval
v =(
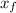 -x₀) / Δt
-x₀) / Δt
let's use this expression for each object
a) Stone
It tells us that it is released from y₀ = 10 ft and reaches the floor at
t = 0.788 s, but in the problem they tell us that the calculation is for t = 1.38 s
 = (0-10) / 1.38
= (0-10) / 1.38
v_{y} = - 7.25 ft / s
in this interval a distance of x_{f} = 0.500 ft was moved away from the building (x₀ = 0 ft)
vₓ = (0.500- 0) / 1.38
vₓ = 0.362 ft / s
In my opinion it makes no sense to keep measuring the time after the stone has stopped.
b) tennis ball
It leaves the building at a height of y₀= 10ft and at the end of the period it is at a height of y_{f} = 5.63 ft, all this in a time of t = 0.788 + 0.591 = 1.38 s
the average vertical speed is
 = (5.63 - 10) / 1.38
= (5.63 - 10) / 1.38
v_{y} = -3.16 ft / s
for horizontal velocity the ball leaves the building xo = 0 reaches the floor
x₁ = 0.500 foot and when bouncing it travels x₂ = 0.375 foot, therefore the distance traveled
x_{f} = x₁ + x₂
x_{f} = 0.500 + 0.375
x_{f} = 0.875 ft
we calculate
vₓ = (0.875 - 0) / 1.38
vₓ = 0.634 ft / s
c) The golf ball
the vertical displacement y₀ = 10 ft, and y_{f} = 7.88 ft
v_{y} = (7.88 - 10) / 1.38
v_{y} = - 1,536 ft / s
the horizontal displacement x₀ = 0 ft to the point xf = 0.875 ft
vₓ = (0.875 -0) / 1.38
vₓ = 0.634 ft / s
2) in this part we are asked for the instantaneous speed at the end of the time interval
a) the stone is stopped so its speed is zero
v_{y} = vₓ = 0
b) the tennis ball
It is at its maximum height so its vertical speed is zero
v_{y} = 0
horizontal speed does not change
vₓ = 0.634 ft / s
c) The golf ball
they do not indicate that it is still rising. Therefore its vertical speed is greater than zero
v_{y} > 0
horizontal speed is constant
vₓx = 0.634 ft / s
the total velocity of the object can be found with the Pythagorean theorem
v = √ (vₓ² + v_{y}²)
When reviewing the results, the golf ball is the one with the highest instantaneous speed at the end of the period