Complete Question
From a random sample of size 18, a researcher states that (11.1, 15.7) inches is a 90% confidence interval for mu, the mean length of bass caught in a small lake. A normal distribution was assumed. Using the 90% confidence interval obtain:
a. A point estimate of
 and its 90% margin of error.
and its 90% margin of error.
b. A 95% confidence interval for
 .
.
Answer:
a
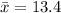 .
.
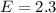
b

Explanation:
From the question we are told that
The sample size is n = 18
The 90% confidence interval is (11.1, 15.7)
Generally the point estimate of
 is mathematically evaluated as
is mathematically evaluated as
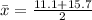
=>
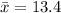
Generally the margin of error is mathematically evaluated as
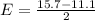
=>
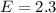
From the question we are told the confidence level is 90% , hence the level of significance is
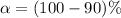
=>
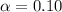
Generally from the normal distribution table the critical value of
 is
is
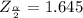
Generally the equation for the lower limit of the confidence interval is
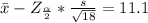
=>
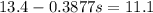
=>
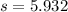
From the question we are told the confidence level is 95% , hence the level of significance is
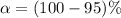
=>

Generally from the normal distribution table the critical value of
 is
is
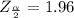
Generally the margin of error is mathematically represented as
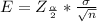
=>
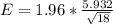
=>
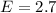
Generally 95% confidence interval is mathematically represented as
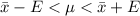
=>
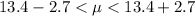
=>
