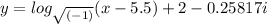Question

Write the logarithmic function that best represents the data below.

Answer 1

`y = log_(√((-1)) ) (x - 5.5) + 2 - 0.25817i`

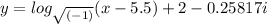
Explanation:

The general form of a logarithmic function is given as follows;

`y = log_b (x - h) + k`

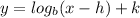
From the given data, we have;

When x = 1, y = -30

Therefore;

`b^(-30 - k) = 1 - h`

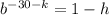
When x = 4, y = 0

Therefore;

`b^(0 - k) = 4 - h`

`b^( - k) = 4 - h`

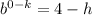
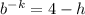
When x = 5, y = 6

Therefore;

`b^(6 - k) = 5 - h`

`b^(6 - k) = b^(6) * b^(- k) = 5 - h`

`\therefore b^(6) =(5 - h)/(b^(- k)) = (5 - h)/(4 - h)`

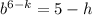
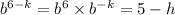
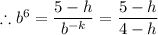
When x = 6, y = 4

Therefore;

`b^(4 - k) = 6 - h`

`b^(4 - k) = b^(4) * b^(- k) = 6 - h`

`\therefore b^(4) = (6 - h)/(b^(- k)) = (6 - h)/(4 - h)`

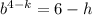
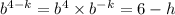
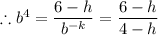
Which gives;

`\therefore (b^(6))/(b^(4)) =b^(2) = ((5 - h)/(4 - h))/((6 - h)/(4 - h)) = (5 - h)/(6 - h)`

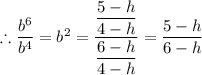
When x = 7, y = 2

Therefore;

`b^(2 - k) = 7 - h`

`b^(2) * b^(- k) = 7 - h`

`\therefore b^(2) =(7 - h)/(4 - h)`

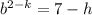
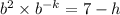
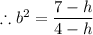
From which we have;

`(5 - h)/(6 - h) = (7 - h)/(4 - h)`

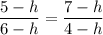
20 - 5·h - 4·h + h² = 42 - 7·h - 6·h + h²

20 - 9·h = 42 - 13·h

4·h = 22

h = 22/4 = 5.5

`\therefore b^(2) =(7 - h)/(4 - h) =(7 - 5.5)/(4 - 5.5) = (1.5)/(-1.5) = -1`

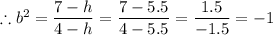
b = √(-1)

`b^( - k) = 4 - h`

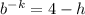
-k = log(-1.5)/log(√-1)

k = 2 - 0.258127·i

The logarithmic function is therefore;

`y = log_(√((-1)) ) (x - 5.5) + 2 - 0.25817i`