Answer:
a)
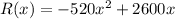
b)
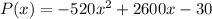
c)x=2.5
d)P(x)=3220
Explanation:
Let Demand function be D=Ax+B
We are given that When you charged $4 the demand was 520 log-ons per month
So, D = 520 , x = 4
So, 520=4A+B ----1
We are also given that When you lowered the price to $3.50, the demand increased to 780 log-ons per month.
So, D=780 , x = 3.50
So, 780=3.5A+B ----2
Substract 2 form 1
4A+B-3.5A-B=520-780
0.5A=-260
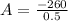
A=-520
Substitute value of A in 2
780=3.5(-520)+B
780-3.5(-520)=B
2600=B
So, D=-520x+2600
Revenue = Demand (x)=(-520x+2600)(x)
a)
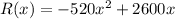
b) Profit = Revenue - cost
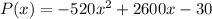
c)to obtain the largest possible monthly profit.
Equate the first derivative of profit to 0
P'(x)=-1040x+2600=0

x=2.5
d)Now to find the largest possible monthly profit
Substitute x = 2.5 in Profit function
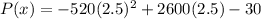
P(x)=3220