Question

2. A tree casts a shadow 25m long. At the same time, a signpost next

to the tree casts a shadow 6m long. The signpost is 3.5m tall. How
tall is the tree?
(10 pts.)

Answer 1

The height of the tree is 14.85
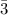`\bar 3` m

Explanation:

The length of the shadow cast by the tree = 25 m

The length of the shadow cast by the signpost = 6 m

The height of the signpost = 3.5 m

Therefore, by similar triangles, we have;

Let θ, represent the angle formed by the line extending a line from the tip of the shadow, to the tip of the object and let x represent the height of the tree, we have

Tan(θ) = Opposite/Adjacent = Height of the object/(The length of the shadow)

∴ Tan(θ) = 3.5/6 = x/25

x = 25 × 3.5/6 = 14.58
`\bar 3`

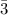
The height of the tree = x = 14.85
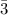`\bar 3` m