Question

2 points

Rheese bought a new car for $17.500. The value of the car is depreciating at a rate of 4.6%
each year. How much would the car be worth in 4 years?
$20,949.07
$79,515.07
$1,488.03
$14,495.44
$14,253.86
quation of the asymptote for the given
Doint

Answer 1

Given:

Initial value of new car = $17,500

Depreciation rate = 4.6%

To find:

The value of car after 4 years.

Solution:

The exponential decay model is

`y=a(1-r)^t`

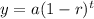
where, a is initial value, r is decreasing rate and t is time in years.

Substitute a=17500, r=0.046 and t=4 in the above equation.

`y=17500(1-0.046)^4`

`y=17500(0.954)^4`

`y=17500(0.8283111)`

`y=14495.44425`

`y\approx 14495.44`

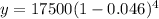
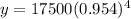
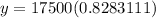
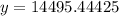
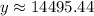
The value of car after 4 years is $14495.44.

Therefore, the correct option is D.