Question

find the value of x of given figure and solve this question step by step plzz help question number D​​

Answer 1

The value of x is 15 cm.

Explanation:

There are two triangles in the diagram that share a common side.

The triangles are:

ABC and BDC

First we have to find the third side of BDC so that we can use it to find the value of x.

The triangle is a right angled triangle so Pythagoras theorem can be used to find the third side.

In the triangle

`Base = BD =10cm\\Hypotenuse = BC = ?\\Perpendicular = CD = 2√(11)cm`

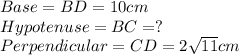
Pythagoras theorem is given as:

`(Hypotenuse)^2 = (Base)^2 + (Perpendicular)^2\\BC^2 = BD^2 + CD^2\\BC^2 = (10)^2 + (2√(11))^2\\BC^2 = 100+(2^2 * 11)\\BC^2 = 100+(4*11)\\BC^2 = 100+44\\BC^2 = 144\\√(BC^2) = √(144)\\BC = 12cm`

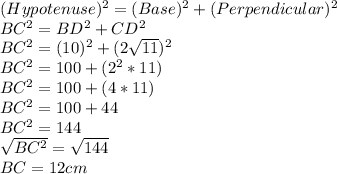
Now for triangle ABC

`Base = BC = 12 cm\\Perpendicular = AB = 9 cm\\Hypotenuse = AC = x\\`

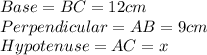
Using Pythagoras theorem

`AC^2 = BC^2+AB^2\\x^2 = (12)^2 + (9)^2\\x^2 = 144+81\\x^2 = 225\\√(x^2) = √(225)\\x = 15cm`

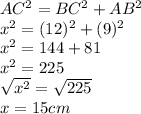
Hence,

The value of x is 15 cm.

Answer 2

15

Explanation:

First we need to find the length of BC and for that we gonna use Pysagoras theorem

10^2 + (2√11)^2 = |BC|^2

√144 = |BC|^2

12 = BC Now we will use this to find the value of x

x^2 = 12^2 + 9^2

x^2 = 144 + 81

x^2 = 225

√x^2 = √225

x = 15