Answer:
9, 11, 13.
Explanation:
Let the first positive odd integer be x.
Hence, the three consecutive odd integers will be x, (x + 2), and (x + 4).
The square of the middle integer increased by four times the largest integer is 173. In other words:
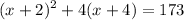
Solve for x:
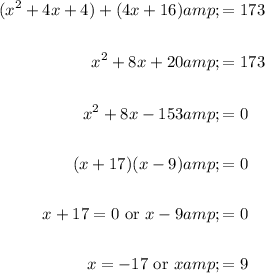
Because the integers must be positive, we can ignore the first solution.
In conclusion, our three consecutive odd integers are 9, 11, 13.