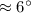Question

To aid in sea navigation, Little Gull Island Lighthouse shines a light from a height of 91 feet above sea level with an unknown angle of depression. If the beam of light shines on the sea surface at a point that is 865 feet away from the base of the lighthouse, what is the angle of depression?

Answer 1

`\approx 6^\circ`

Explanation:

Given that:

Little Gull Island Lighthouse shines a light from a height of 91 feet above the sea level.

The angle of depression is unknown.

Distance of the point at sea surface from the base of lighthouse is 865 ft.

This situation can be modeled or can be represented as the figure attached in the answer area.

The situation can be represented by a right angled
`\triangle ABC` in which we are given the base and the height of the triangle.

And we have to find the value of
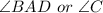`\angle BAD \ or \ \angle C` (Because they are the internal vertically opposite angles).

Using tangent ratio:

`tan\theta = (Perpendicular)/(Base)`

`tanC = (AC)/(BC)\\\Rightarrow tanC = (91)/(865)\\\Rightarrow tanC = 0.105\\\Rightarrow \angle C \approx 6^\circ`

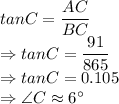
Therefore, the angle of depression is:
`\approx 6^\circ`