Answer:
A
Explanation:
To reflect a function over the x-axis, we multiply the function by -1. So, if f(x) is the original function, then -f(x) is the function across the x-axis.
To reflect a function over the y-axis, we multiply the inside of the function by -1. So, if f(x) is the original function, then f(-x) is the function across the x-axis.
We have:
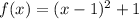
Then:

We can see that the choice that resembles this is A. If we let:
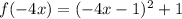
This is a reflection over the y-axis followed by a horizontal compression by a factor of 4.
Hence, our answer is A.